FICHE DE RÉVISION – Les Fonctions trigonométriques
(Niveau : Première)
Analyse : Fonctions Trigonométriques
Du cercle aux vagues : comprendre le radian, le cercle trigonométrique et les fonctions sinus et cosinus.
Partie 1 : Le Cercle Trigonométrique et le Radian
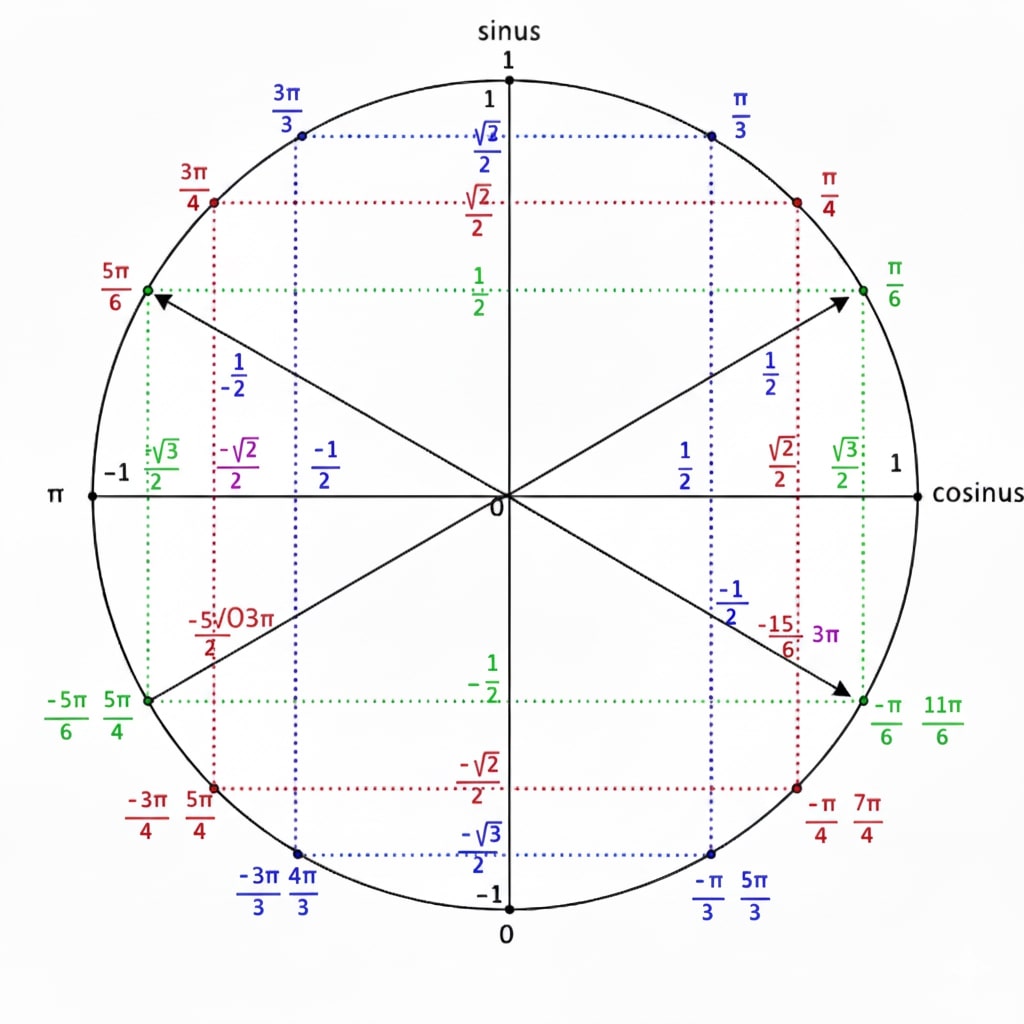
1. Le Cercle Trigonométrique
Le cercle trigonométrique (souvent appelé « cercle trigo ») est un cercle très spécial :
- Son centre est l’origine du repère \(O(0, 0)\).
- Son rayon est \(R = 1\).
- On lui ajoute un sens de parcours : le sens direct (ou trigonométrique) est le sens inverse des aiguilles d’une montre (positif +). Le sens indirect est le sens horaire (négatif -).
Le point de départ pour mesurer les angles est le point \(I(1, 0)\).
2. Le Radian
Au lieu des degrés, on utilise une nouvelle unité d’angle : le radian (rad).
Un angle mesure 1 radian si, sur le cercle trigonométrique (rayon 1), il intercepte un arc de longueur 1.
Conversion fondamentale (Tour complet) :
Un tour complet = \(360^\circ\) = Longueur du cercle (périmètre) = \(2\pi R = 2\pi \times 1 = 2\pi\) radians.
$$ 360^\circ = 2\pi \text{ rad} $$
$$ 180^\circ = \pi \text{ rad} $$
Pour convertir : On utilise la proportionnalité.
Degrés vers Radians : \(\text{Angle}_{\text{rad}} = \text{Angle}_{\text{deg}} \times \frac{\pi}{180}\)
Radians vers Degrés : \(\text{Angle}_{\text{deg}} = \text{Angle}_{\text{rad}} \times \frac{180}{\pi}\)
\(90^\circ = 90 \times \frac{\pi}{180} = \frac{\pi}{2}\) rad.
\(60^\circ = 60 \times \frac{\pi}{180} = \frac{\pi}{3}\) rad.
\(45^\circ = 45 \times \frac{\pi}{180} = \frac{\pi}{4}\) rad.
\(30^\circ = 30 \times \frac{\pi}{180} = \frac{\pi}{6}\) rad.
\(\frac{3\pi}{2}\) rad \( = \frac{3\pi}{2} \times \frac{180}{\pi} = 3 \times 90 = 270^\circ\).
Partie 2 : Enroulement de la Droite et Définition de Cosinus/Sinus
1. Enroulement de la Droite Réelle
Imagine une droite numérique verticale, dont le 0 est placé sur le point \(I(1, 0)\) du cercle trigo. On « enroule » cette droite autour du cercle :
- Les nombres positifs s’enroulent dans le sens direct (+).
- Les nombres négatifs s’enroulent dans le sens indirect (-).
À chaque nombre réel \(x\), on associe un unique point \(M\) sur le cercle trigonométrique. Ce point \(M\) est l’image de \(x\) sur le cercle.
L’angle (en radians) entre le vecteur \(\vec{OI}\) et le vecteur \(\vec{OM}\) est égal à \(x\).
Comme un tour complet fait \(2\pi\), les points images de \(x\), \(x+2\pi\), \(x-2\pi\), \(x+4\pi\)… sont confondus. Tous les nombres de la forme \(x + k \times 2\pi\) (où \(k\) est un entier relatif) ont le même point image \(M\).
Le point image de \(\pi/2\) est le point \(J(0, 1)\) (quart de tour positif).
Le point image de \(\pi\) est le point \(I'(-1, 0)\) (demi-tour positif).
Le point image de \(-\pi/2\) est le point \(J'(0, -1)\) (quart de tour négatif).
Le point image de \(5\pi/2 = \pi/2 + 2\pi\) est le même que celui de \(\pi/2\), soit \(J(0, 1)\).
2. Définition du Cosinus et du Sinus d’un Réel
Soit \(x\) un nombre réel et \(M\) son point image sur le cercle trigonométrique dans un repère orthonormé \((O; \vec{i}, \vec{j})\).
Par définition :
- Le cosinus de \(x\), noté \(\cos(x)\), est l’abscisse du point \(M\).
- Le sinus de \(x\), noté \(\sin(x)\), est l’ordonnée du point \(M\).
Comme M est sur le cercle de rayon 1 (\(OM=1\)), ses coordonnées vérifient l’équation du cercle \(X^2 + Y^2 = 1\). D’où la relation fondamentale :
$$ \cos^2(x) + \sin^2(x) = 1 $$De plus, comme les coordonnées d’un point sur le cercle unité sont comprises entre -1 et 1 :
$$ -1 \le \cos(x) \le 1 \quad \text{et} \quad -1 \le \sin(x) \le 1 $$3. Valeurs Remarquables (À SAVOIR PAR CŒUR !)
Tu dois connaître le cosinus et le sinus des angles \(0, \pi/6, \pi/4, \pi/3, \pi/2\).
| \(x\) (rad) | 0 | \(\pi/6\) (30°) | \(\pi/4\) (45°) | \(\pi/3\) (60°) | \(\pi/2\) (90°) |
|---|---|---|---|---|---|
| \(\cos(x)\) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | 0 |
| \(\sin(x)\) | 0 | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | 1 |
Pour le Sinus : Écris \(\frac{\sqrt{0}}{2}, \frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}\). Simplifie, et tu as la ligne du sinus ! (0, 1/2, \(\sqrt{2}/2\), \(\sqrt{3}/2\), 1).
Pour le Cosinus : C’est la même ligne, mais lue à l’envers !
Démonstration (Valeurs pour \(\pi/4\), \(\pi/3\))
Pour \(x = \pi/4\) (45°) :
Le point M forme un triangle OMH (H projeté sur l’axe Ox) qui est isocèle rectangle en H (angles 45°, 45°, 90°).
Donc \(OH = MH\), ce qui signifie \(\cos(\pi/4) = \sin(\pi/4)\).
On utilise \(\cos^2(x) + \sin^2(x) = 1\).
\(\cos^2(\pi/4) + \cos^2(\pi/4) = 1 \Rightarrow 2\cos^2(\pi/4) = 1 \Rightarrow \cos^2(\pi/4) = 1/2\).
Comme \(\pi/4\) est dans le premier quadrant, son cosinus est positif.
\(\cos(\pi/4) = \sqrt{1/2} = 1/\sqrt{2} = \sqrt{2}/2\). Et donc \(\sin(\pi/4) = \sqrt{2}/2\).
Pour \(x = \pi/3\) (60°) :
Le point M forme un triangle OIM’ (M’ symétrique par rapport à Ox) qui est équilatéral (angles 60°, 60°, 60°).
Le projeté H de M sur Ox est le milieu de [OI’]. Non, ça c’est pour \(\pi/6\).
Considérons le triangle OMH rectangle en H. L’angle en O est \(\pi/3\). L’angle en M est \(\pi/2 – \pi/3 = \pi/6\).
Dans ce triangle, on sait (ou on admet via la géométrie du triangle équilatéral) que le côté opposé à l’angle \(\pi/6\) (soit OH) est la moitié de l’hypoténuse (OM=1).
Donc \(OH = 1/2\). Or \(OH = \cos(\pi/3)\). Donc \(\cos(\pi/3) = 1/2\).
On utilise \(\cos^2(x) + \sin^2(x) = 1\).
\((1/2)^2 + \sin^2(\pi/3) = 1 \Rightarrow 1/4 + \sin^2(\pi/3) = 1 \Rightarrow \sin^2(\pi/3) = 1 – 1/4 = 3/4\).
Comme \(\pi/3\) est dans le premier quadrant, son sinus est positif.
\(\sin(\pi/3) = \sqrt{3/4} = \sqrt{3}/2\).
Partie 3 : Fonctions Cosinus et Sinus
On définit maintenant les fonctions qui à tout réel \(x\) associent \(\cos(x)\) et \(\sin(x)\).
1. Propriétés (Parité et Périodicité)
Parité :
- Les points images de \(x\) et \(-x\) sont symétriques par rapport à l’axe des abscisses. Ils ont la même abscisse et des ordonnées opposées.
Donc : \( \cos(-x) = \cos(x) \) \(\Rightarrow\) La fonction cosinus est paire.
\( \sin(-x) = -\sin(x) \) \(\Rightarrow\) La fonction sinus est impaire.
Périodicité :
- Les nombres \(x\) et \(x + 2\pi\) ont le même point image sur le cercle.
Donc : \( \cos(x + 2\pi) = \cos(x) \) et \( \sin(x + 2\pi) = \sin(x) \).
Les fonctions cosinus et sinus sont périodiques de période \(2\pi\). (Le motif se répète tous les \(2\pi\)).
Conséquence : Pour étudier ces fonctions, il suffit de les étudier sur un intervalle de longueur \(2\pi\) (ex: \([-\pi, \pi]\) ou \([0, 2\pi]\)) et d’utiliser la parité. On étudie souvent sur \([0, \pi]\) puis on complète par symétrie.
2. Courbes Représentatives (Sinusoïdes)
Les courbes des fonctions cosinus et sinus s’appellent des sinusoïdes. Ce sont des vagues infinies.
Courbe de \(y = \cos(x)\) :
– Paire : Symétrique par rapport à l’axe (Oy).
– Passe par (0, 1).
– Oscille entre -1 et 1.
[Image of the graph of y=cos(x)]
Courbe de \(y = \sin(x)\) :
– Impaire : Symétrique par rapport à l’origine O.
– Passe par (0, 0).
– Oscille entre -1 et 1.
[Image of the graph of y=sin(x)]
On remarque que la courbe de sinus est juste la courbe de cosinus décalée de \(\pi/2\) vers la droite.
Imagine le point M qui fait le tour du cercle trigo.
Son abscisse (\(\cos x\)) commence à 1 (pour x=0), descend à 0 (\(x=\pi/2\)), descend à -1 (\(x=\pi\)), remonte à 0 (\(x=3\pi/2\)), remonte à 1 (\(x=2\pi\))… C’est la vague cosinus !
Son ordonnée (\(\sin x\)) commence à 0 (pour x=0), monte à 1 (\(x=\pi/2\)), descend à 0 (\(x=\pi\)), descend à -1 (\(x=3\pi/2\)), remonte à 0 (\(x=2\pi\))… C’est la vague sinus !
Partie 4 : Angles Associés
Ce sont des formules (à retrouver sur le cercle !) qui permettent de calculer le cos/sin d’angles liés à \(x\) (\(-x, \pi-x, \pi+x, \pi/2-x, \pi/2+x\)…).
En observant les symétries sur le cercle trigonométrique, on retrouve facilement :
- \(\cos(-x) = \cos(x)\)
- \(\sin(-x) = -\sin(x)\)
- \(\cos(\pi – x) = -\cos(x)\)
- \(\sin(\pi – x) = \sin(x)\)
- \(\cos(\pi + x) = -\cos(x)\)
- \(\sin(\pi + x) = -\sin(x)\)
- \(\cos(\pi/2 – x) = \sin(x)\)
- \(\sin(\pi/2 – x) = \cos(x)\)
- \(\cos(\pi/2 + x) = -\sin(x)\)
- \(\sin(\pi/2 + x) = \cos(x)\)
Calculer \(\cos(2\pi/3)\).
On écrit \(2\pi/3 = \pi – \pi/3\).
\(\cos(2\pi/3) = \cos(\pi – \pi/3) = -\cos(\pi/3) = -1/2\).
Calculer \(\sin(-\pi/6)\).
\(\sin(-\pi/6) = -\sin(\pi/6) = -1/2\).
Partie 5 : Entraînement (Exercices)
-
Exercice 1 (Conversions et Placement) :
a) Convertir \(150^\circ\) en radians.
b) Convertir \(5\pi/6\) radians en degrés.
c) Placer approximativement sur le cercle trigonométrique les points images des réels \( \pi/3 \), \(-\pi/4\), \(3\pi/2\), \(5\pi\). -
Exercice 2 (Valeurs remarquables et associées) : Donner la valeur exacte de :
a) \(\sin(3\pi/4)\) (Indice : \(3\pi/4 = \pi – \pi/4\))
b) \(\cos(7\pi/6)\) (Indice : \(7\pi/6 = \pi + \pi/6\))
c) \(\cos(-\pi/3)\)
d) \(\sin(5\pi/2)\) -
Exercice 3 (Lien Graphe-Cercle) :
a) Sur la courbe de \(y=\cos x\), où retrouve-t-on la périodicité \(2\pi\) ?
b) Sur la courbe de \(y=\sin x\), comment voit-on que la fonction est impaire ?
Partie 6 : Corrections Détaillées
Correction Exercice 1 (Conversions et Placement)
a) \(150^\circ\) en radians :
\(150 \times \frac{\pi}{180} = 15 \times \frac{\pi}{18} = 5 \times \frac{\pi}{6} = \frac{5\pi}{6}\) rad.
b) \(5\pi/6\) rad en degrés :
\(\frac{5\pi}{6} \times \frac{180}{\pi} = 5 \times \frac{180}{6} = 5 \times 30 = 150^\circ\).
c) Placement sur le cercle : (Faire un dessin)
– \(\pi/3\) : Angle de 60° dans le sens +.
– \(-\pi/4\) : Angle de 45° dans le sens -.
– \(3\pi/2\) : Angle de 270° dans le sens + (arrive sur J'(0, -1)).
– \(5\pi = \pi + 2\times 2\pi\) : Fait deux tours complets puis un demi-tour. Arrive au même point que \(\pi\), soit I'(-1, 0).
Correction Exercice 2 (Valeurs remarquables et associées)
a) \(\sin(3\pi/4)\) :
\(\sin(3\pi/4) = \sin(\pi – \pi/4) = \sin(\pi/4) = \frac{\sqrt{2}}{2}\).
b) \(\cos(7\pi/6)\) :
\(\cos(7\pi/6) = \cos(\pi + \pi/6) = -\cos(\pi/6) = -\frac{\sqrt{3}}{2}\).
c) \(\cos(-\pi/3)\) :
\(\cos(-\pi/3) = \cos(\pi/3) = \frac{1}{2}\).
d) \(\sin(5\pi/2)\) :
\(5\pi/2 = \pi/2 + 4\pi/2 = \pi/2 + 2\pi\).
\(\sin(5\pi/2) = \sin(\pi/2 + 2\pi) = \sin(\pi/2) = 1\).
Correction Exercice 3 (Lien Graphe-Cercle)
a) Périodicité sur \(y=\cos x\) :
Le motif de la courbe (la forme de la vague) se répète exactement tous les \(2\pi\) sur l’axe des abscisses. Par exemple, le motif entre \(x=0\) et \(x=2\pi\) est identique à celui entre \(x=2\pi\) et \(x=4\pi\).
b) Imparité sur \(y=\sin x\) :
La courbe est symétrique par rapport à l’origine O(0,0). Si on fait tourner la courbe d’un demi-tour (180°) autour de O, elle se superpose parfaitement à elle-même.
Besoin d'aide en mathématiques ?
Je propose des cours de remise à niveau en visio ou en présentiel

