FICHE DE RÉVISION – Nombres et calculs : Utiliser le calcul littéral
(Niveau : Seconde)
Calcul Littéral et Inéquations
La boîte à outils essentielle : développer, factoriser, résoudre des équations et maîtriser les inéquations.
Partie 1 : Puissances, Racines et Valeur Absolue
C’est une révision rapide des outils de base vus dans les chapitres précédents, mais essentiels pour le calcul littéral.
- Puissances : Les règles \((a^n)^m = a^{nm}\) et \(a^n \times a^m = a^{n+m}\) s’appliquent aussi avec des variables (lettres).
- Racines carrées : La règle principale est \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) (pour \(a, b \ge 0\)).
C’est un point nouveau et très important ! Que vaut \(\sqrt{a^2}\) ?
On pourrait penser que c’est \(a\), mais c’est faux si \(a\) est négatif.
Exemple : \(\sqrt{(-5)^2} = \sqrt{25} = 5\). On n’obtient pas -5 !
La règle correcte, qui marche pour tous les réels, est : $$\sqrt{a^2} = |a|$$ (La racine carrée de \(a^2\) est la valeur absolue de \(a\).)
Partie 2 : Les Identités Remarquables
C’est le cœur de ce chapitre. Tu dois les connaître par cœur dans les deux sens : pour développer (passer d’une multiplication à une somme) et pour factoriser (passer d’une somme à une multiplication).
1. Carré d’une somme :
$$(a + b)^2 = a^2 + 2ab + b^2$$
Développer : \((x + 3)^2 = x^2 + 2(x)(3) + 3^2 = x^2 + 6x + 9\)
Factoriser : \(x^2 + 10x + 25 = x^2 + 2(x)(5) + 5^2 = (x + 5)^2\)
2. Carré d’une différence :
$$(a – b)^2 = a^2 – 2ab + b^2$$
Développer : \((2x – 5)^2 = (2x)^2 – 2(2x)(5) + 5^2 = 4x^2 – 20x + 25\)
Factoriser : \(9x^2 – 12x + 4 = (3x)^2 – 2(3x)(2) + 2^2 = (3x – 2)^2\)
3. Différence de deux carrés :
$$a^2 – b^2 = (a – b)(a + b)$$
Développer : \((x – 7)(x + 7) = x^2 – 7^2 = x^2 – 49\)
Factoriser : \(16x^2 – 81 = (4x)^2 – 9^2 = (4x – 9)(4x + 9)\)
Sans elles, tu seras bloqué partout, tout le temps. C’est comme essayer de faire du vélo sans chaîne.
Comment choisir la forme ? C’est la compétence clé.
- Je veux résoudre une équation (ex: \(f(x) = 0\)) : J’utilise la forme FACTORISÉE (équation produit-nul).
- Je veux calculer une image, ou comparer : J’utilise souvent la forme DÉVELOPPÉE.
Partie 3 : Équations et Inéquations du 1er degré
Une équation (avec \(=\)) ou inéquation (avec \(<\), \(>\), \(\le\), \(\ge\)) du premier degré, c’est quand l’inconnue \(x\) n’a pas de puissance (ou puissance 1).
1. Équations (Rappel)
On isole l’inconnue \(x\) en « déplaçant » les nombres de l’autre côté : ce qui est additionné devient soustrait, ce qui multiplie devient divisé.
Résoudre \(4x – 5 = 11\)
\(4x = 11 + 5\)
\(4x = 16\)
\(x = \frac{16}{4}\)
\(x = 4\). L’ensemble solution est \(S = \{4\}\).
2. Inéquations (Nouveau)
La méthode est la même que pour les équations, avec UNE SEULE RÈGLE EN OR à respecter.
Quand on multiplie ou divise les deux côtés d’une inéquation par un nombre NÉGATIF, on doit INVERSER LE SENS de l’inégalité.
(\(<\) devient \(>\) , \(\le\) devient \(\ge\), etc.)
Résoudre \( -3x + 7 \le 19 \)
\(-3x \le 19 – 7\)
\(-3x \le 12\)
On va diviser par -3 (un nombre négatif), donc on inverse le sens \(\le\) en \(\ge\) :
\(x \ge \frac{12}{-3}\)
\(x \ge -4\).
L’ensemble solution est \(S = [-4, +\infty[\) (tous les nombres plus grands ou égaux à -4).
Partie 4 : Applications et Stratégies
1. Isoler une variable dans une formule
C’est la même technique que pour les équations. On te donne une formule (physique, géométrie…) et on te demande d’exprimer une lettre en fonction des autres.
Objectif : Isoler la variable demandée.
1. Formule : \(U = R \times I\). Exprimer \(I\).
On divise par \(R\) : \(I = \frac{U}{R}\)
2. Formule : \(V = \pi r^2 h\). Exprimer \(h\).
On divise par \(\pi r^2\) : \(h = \frac{V}{\pi r^2}\)
3. Formule : \(2x + 3y = 5\). Exprimer \(y\).
\(3y = 5 – 2x\)
\(y = \frac{5 – 2x}{3}\) (c’est une équation de droite !)
2. Comparer deux quantités
Pour comparer deux nombres \(A\) et \(B\), on a deux méthodes principales :
Méthode 1 (La plus fréquente) : Étudier le signe de la différence \(A – B\).
Si \(A – B > 0\), alors \(A > B\).
Si \(A – B < 0\), alors \(A < B\).
Si \(A – B = 0\), alors \(A = B\).
Méthode 2 (Si A et B sont positifs) : Comparer le quotient \(\frac{A}{B}\) à 1.
Si \(\frac{A}{B} > 1\), alors \(A > B\).
Si \(\frac{A}{B} < 1\), alors \(A < B\).
Comparer \((x+1)^2\) et \(x^2 + 1\) (pour \(x > 0\)).
On calcule la différence : \(A – B = (x+1)^2 – (x^2 + 1)\)
On développe : \(A – B = (x^2 + 2x + 1) – x^2 – 1\)
On simplifie : \(A – B = 2x\)
Comme on nous a dit que \(x > 0\), alors \(2x > 0\).
Puisque la différence \(A – B\) est positive, on conclut que \(A > B\), donc \((x+1)^2 > x^2 + 1\).
Partie 5 : Démonstrations Clés (Au Programme)
Ces démonstrations t’aident à comprendre d’où viennent les règles.
Démonstration : \(\sqrt{ab} = \sqrt{a}\sqrt{b}\) (pour \(a, b \ge 0\))
Objectif : Prouver que \(\sqrt{ab}\) et \(\sqrt{a}\sqrt{b}\) sont le même nombre.
1. Par définition, la racine carrée d’un nombre \(X\) est le nombre positif qui, mis au carré, donne \(X\).
2. Regardons le nombre \(Y = \sqrt{a}\sqrt{b}\). Comme \(a\) et \(b\) sont positifs, \(\sqrt{a}\) et \(\sqrt{b}\) sont positifs. Leur produit \(Y\) est donc positif.
3. Mettons ce nombre \(Y\) au carré :
\(Y^2 = (\sqrt{a}\sqrt{b})^2\)
\(Y^2 = (\sqrt{a})^2 \times (\sqrt{b})^2\) (règle des puissances)
\(Y^2 = a \times b = ab\)
Conclusion :
Le nombre \(Y = \sqrt{a}\sqrt{b}\) est positif et son carré est \(ab\).
Il est donc, par définition, la racine carrée de \(ab\).
On a bien prouvé que \(\sqrt{ab} = \sqrt{a}\sqrt{b}\).
Démonstration (Piège) : \(\sqrt{a+b} < \sqrt{a} + \sqrt{b}\)
On l’a déjà vu dans la « fiche-attention », c’est le piège classique. Prouvons-le pour \(a > 0, b > 0\).
1. On compare les deux nombres positifs \(A = \sqrt{a+b}\) et \(B = \sqrt{a} + \sqrt{b}\).
Puisqu’ils sont positifs, on peut comparer leurs carrés \(A^2\) et \(B^2\).
2. Calculons \(A^2\) :
\(A^2 = (\sqrt{a+b})^2 = a+b\)
3. Calculons \(B^2\) (avec une identité remarquable) :
\(B^2 = (\sqrt{a} + \sqrt{b})^2\)
\(B^2 = (\sqrt{a})^2 + 2\sqrt{a}\sqrt{b} + (\sqrt{b})^2\)
\(B^2 = a + 2\sqrt{ab} + b\)
4. Comparons \(A^2\) et \(B^2\) :
\(A^2 = a + b\)
\(B^2 = (a + b) + 2\sqrt{ab}\)
On voit clairement que \(B^2\) est plus grand que \(A^2\) (puisqu’on ajoute \(2\sqrt{ab}\), qui est un nombre positif).
Conclusion :
Puisque \(B^2 > A^2\), et que \(A\) et \(B\) sont positifs, on peut conclure que \(B > A\).
Donc \(\sqrt{a} + \sqrt{b} > \sqrt{a+b}\).
Illustration Géométrique de \((a+b)^2 = a^2 + 2ab + b^2\)
Imagine un grand carré dont le côté mesure \((a+b)\).
L’aire totale de ce grand carré est : \((a+b) \times (a+b) = (a+b)^2\).
Maintenant, coupons ce grand carré en quatre morceaux (trace un trait vertical et un trait horizontal à l’intérieur) :
- Un petit carré en haut à gauche, de côté \(a\). Son aire est \(a^2\).
- Un petit carré en bas à droite, de côté \(b\). Son aire est \(b^2\).
- Un rectangle en haut à droite, de côtés \(a\) et \(b\). Son aire est \(ab\).
- Un rectangle en bas à gauche, de côtés \(a\) et \(b\). Son aire est \(ab\).
L’aire totale est aussi la somme des aires de ces quatre morceaux :
Aire = \(a^2 + b^2 + ab + ab\)
Aire = \(a^2 + 2ab + b^2\)
Conclusion :
Puisque l’aire totale est la même, on a bien prouvé géométriquement que :
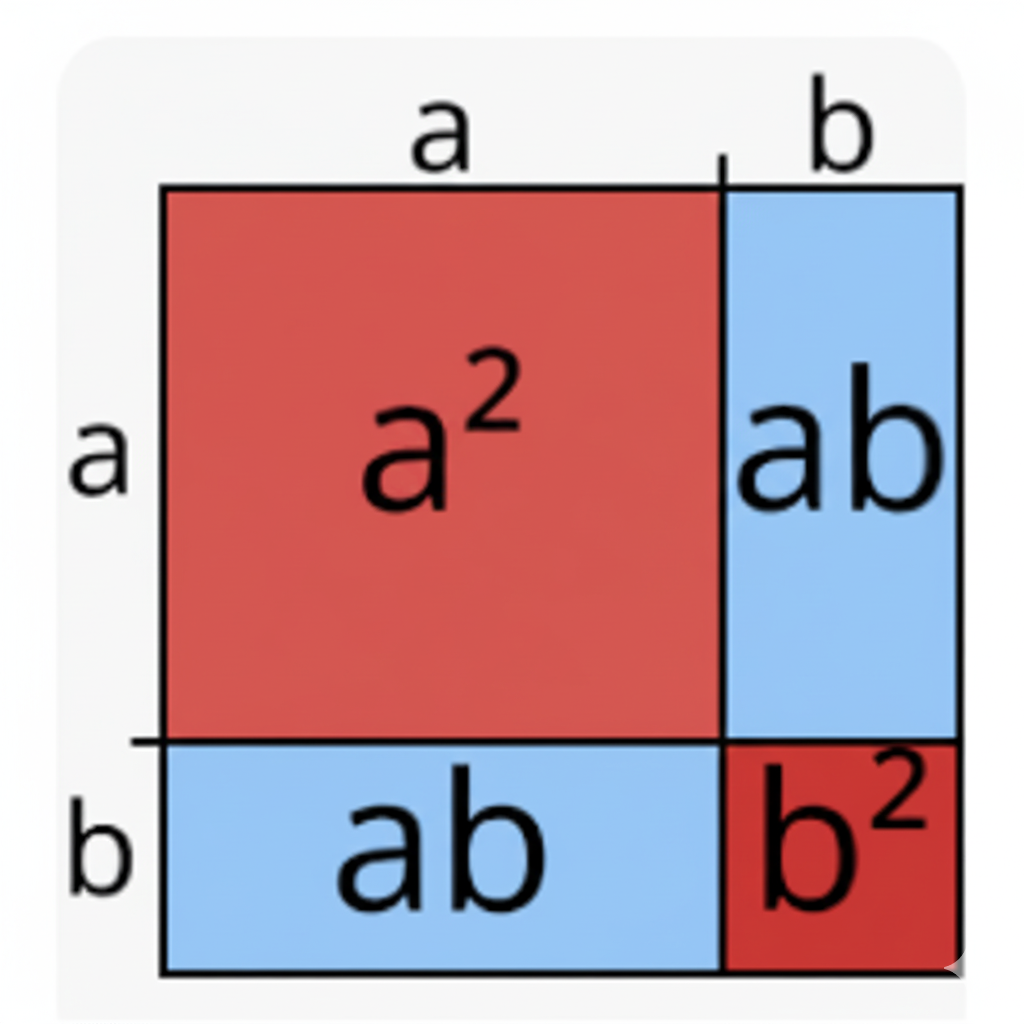
Partie 6 : Entraînement (Exercices)
À toi de jouer ! Ces exercices couvrent les capacités attendues au programme.
-
Exercice 1 (Identités) :
a) Développer et réduire \( (3x – 4)^2 \).
b) Factoriser au maximum \( 25x^2 – 49 \). -
Exercice 2 (Inéquation) :
Résoudre dans \(\mathbb{R}\) l’inéquation \( 2x – 7 > 5x + 2 \). Donner la solution sous forme d’intervalle. -
Exercice 3 (Isoler une variable) :
On donne la relation \( 5x – 2y = 8 \). Exprimer \(y\) en fonction de \(x\). -
Exercice 4 (Modélisation) :
Mathéo veut louer une voiture.
Agence A : Forfait de 50€, puis 0,20€ par km.
Agence B : Pas de forfait, mais 0,30€ par km.
Modéliser ce problème par une inéquation pour trouver à partir de combien de km l’agence A est plus avantageuse que l’agence B.
Partie 7 : Corrections Détaillées
Cliquez sur chaque exercice pour voir la solution.
Correction Exercice 1 (Identités)
a) Développer :
On utilise \((a-b)^2 = a^2 – 2ab + b^2\) avec \(a=3x\) et \(b=4\).
\((3x – 4)^2 = (3x)^2 – 2(3x)(4) + 4^2\)
Solution : \(9x^2 – 24x + 16\) (N’oublie pas de mettre \(3x\) entre parenthèses au carré !)
b) Factoriser :
On utilise \(a^2 – b^2 = (a-b)(a+b)\) avec \(a^2 = 25x^2\) et \(b^2 = 49\).
Donc \(a = \sqrt{25x^2} = 5x\) et \(b = \sqrt{49} = 7\).
Solution : \((5x – 7)(5x + 7)\)
Correction Exercice 2 (Inéquation)
On veut résoudre \( 2x – 7 > 5x + 2 \).
1. On regroupe les \(x\) à gauche et les nombres à droite :
\(2x – 5x > 2 + 7\)
2. On réduit :
\(-3x > 9\)
3. On divise par -3. Attention, c’est négatif ! On inverse le sens de \(>\) en \(<\).
\(x < \frac{9}{-3}\)
\(x < -3\)
Solution : \( S = ]-\infty, -3[ \)
Correction Exercice 3 (Isoler une variable)
On veut isoler \(y\) dans \( 5x – 2y = 8 \).
1. On isole le bloc avec \(y\) :
\(-2y = 8 – 5x\)
2. On divise tout par -2 :
\(y = \frac{8 – 5x}{-2}\)
3. On « nettoie » l’expression (c’est mieux de ne pas avoir de négatif en bas) :
\(y = \frac{8}{-2} + \frac{-5x}{-2}\)
Solution : \(y = -4 + \frac{5}{2}x\) (ou \(y = 2,5x – 4\))
Correction Exercice 4 (Modélisation)
1. On pose \(x\) = le nombre de km parcourus.
2. On modélise le prix de chaque agence :
Prix Agence A : \(P_A(x) = 50 + 0,20x\)
Prix Agence B : \(P_B(x) = 0,30x\)
3. On veut savoir quand l’agence A est « plus avantageuse », c’est-à-dire quand son prix est inférieur à celui de B :
$$P_A(x) < P_B(x)$$
$$50 + 0,20x < 0,30x$$
4. On résout l’inéquation :
\(50 < 0,30x - 0,20x\)
\(50 < 0,10x\)
On divise par 0,10 (qui est positif, on ne change pas le sens) :
\(\frac{50}{0,10} < x\)
\(500 < x\)
Solution : L’agence A est plus avantageuse (moins chère) si l’on parcourt plus de 500 km.
Besoin d'aide en mathématiques ?
Je propose des cours de remise à niveau en visio ou en présentiel

